The ‘timedatectl‘ command is a new utility for RHEL-based and Debian-based distributions. It is a part of the ‘systemd‘ system and service manager, serving as a replacement for the old traditional date command used in ‘sysvinit‘ daemon-based Linux distributions.
The timedatectl command allows you to query and change the configuration of the system clock and its settings, you can use this command to set or change the current date, time, and timezone or enable automatic system clock synchronization with a remote NTP server.
In this tutorial, am going to take you through the ways you can manage time on your Linux system by setting the date, time, timezone, and synchronize time with NTP from the terminal using the new timedatectl command.
It is always a good practice to maintain the correct time on your Linux server or system and it can have the following advantages:
- maintain a timely operation of system tasks since most tasks in Linux are controlled by time.
- the correct time for logging events and other information on the system and many more.
How to Find and Set Local Timezone in Linux
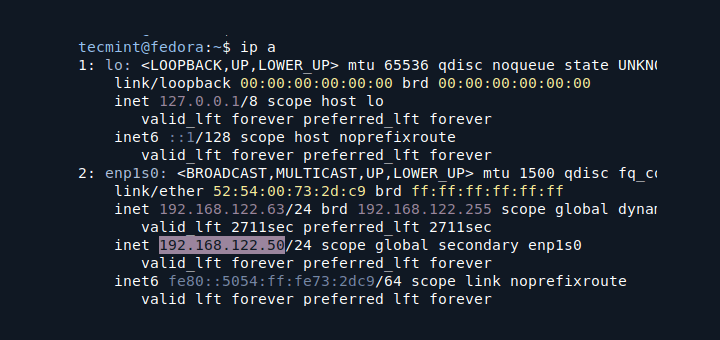
1. To display the current time and date on your system, use the timedatectl command from the command line as follows:
# timedatectl status
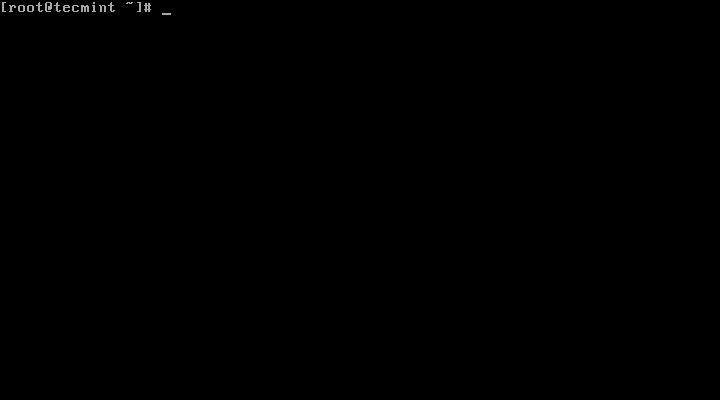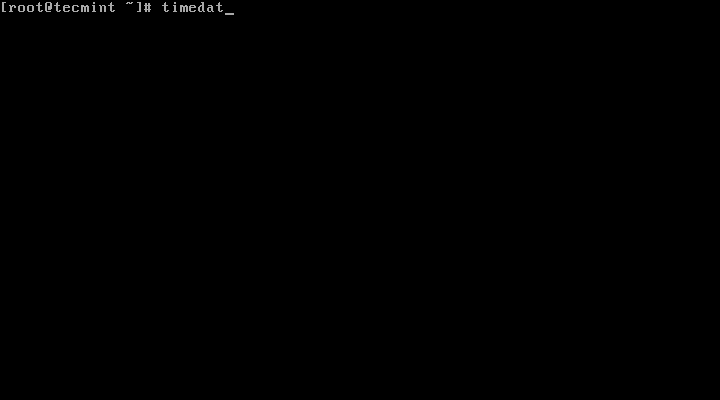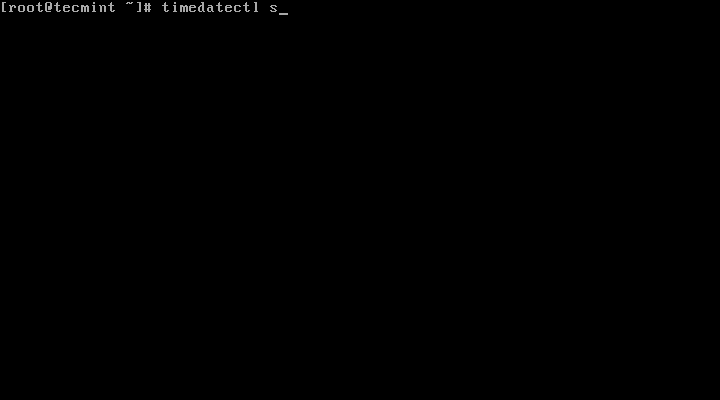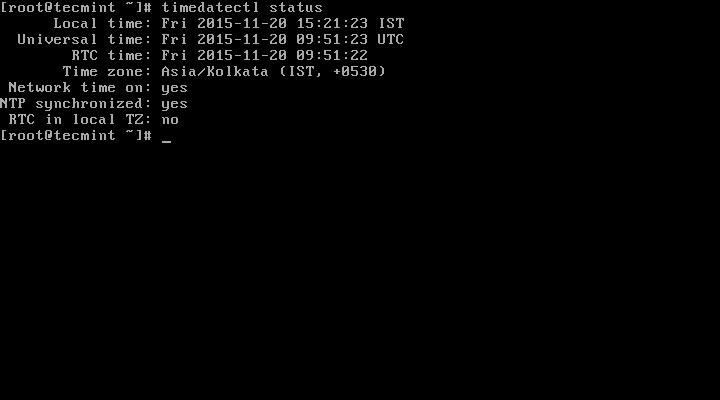
In the screencast above, RTC time is the hardware clock time.
2. The time on your Linux system is always managed through the timezone set on the system, to view your current timezone, do it as follows:
# timedatectl OR # timedatectl | grep Time
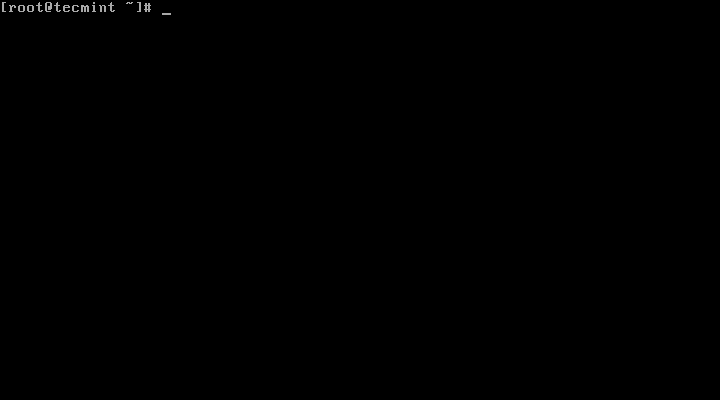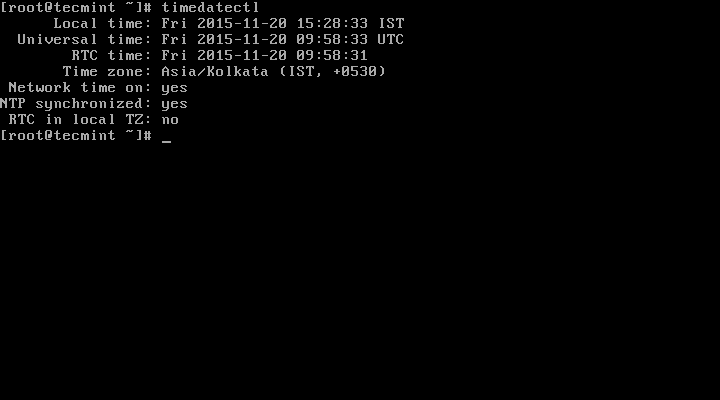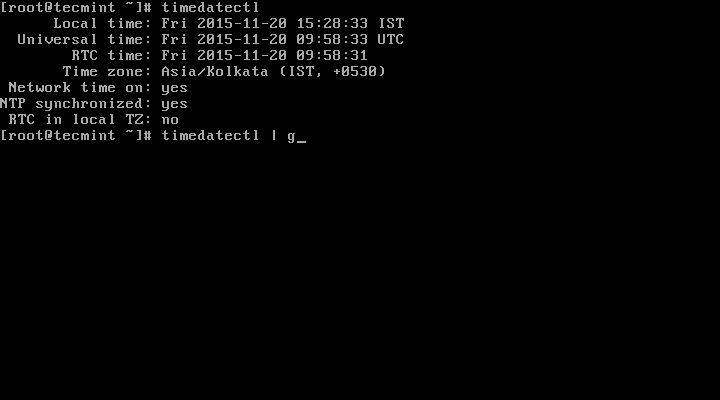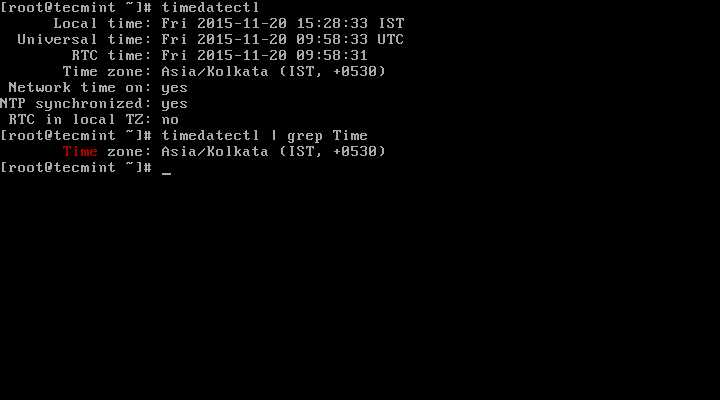
3. To view all available timezones, run the command below:
# timedatectl list-timezones
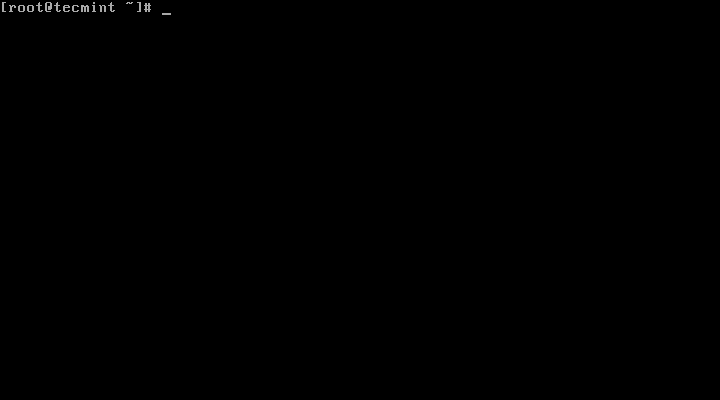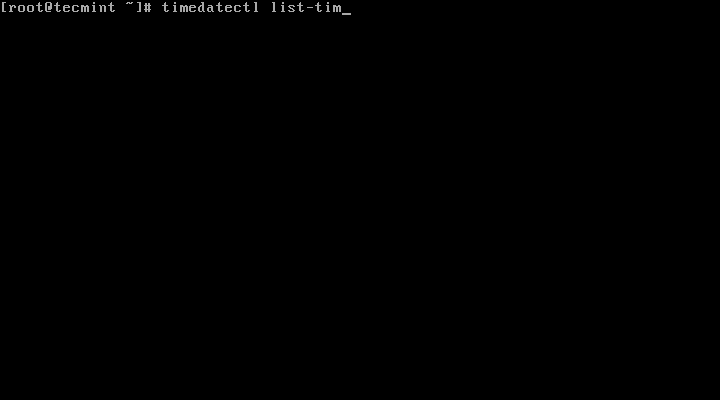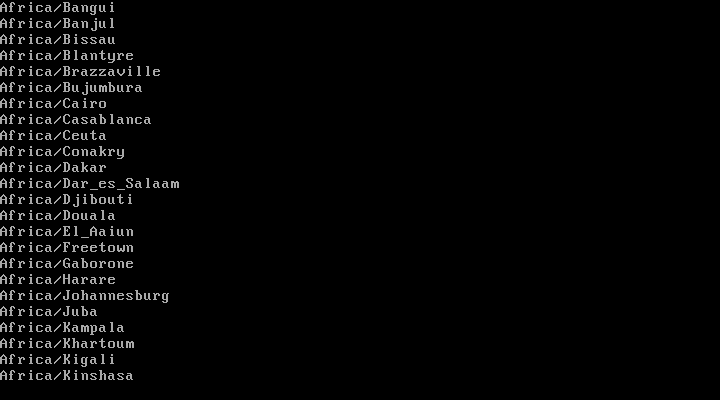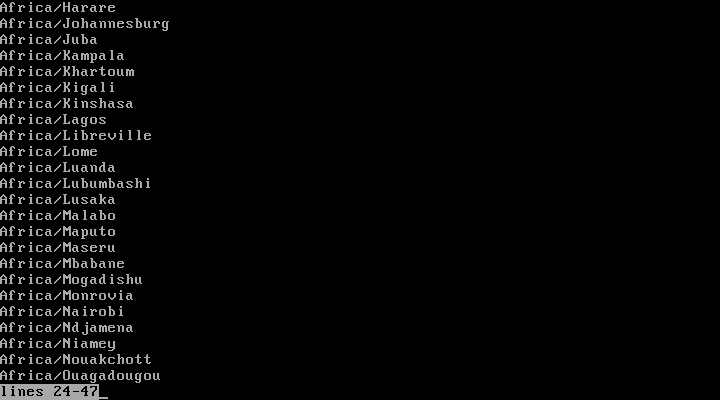
4. To find the local timezone according to your location, run the following command:
# timedatectl list-timezones | egrep -o "Asia/B.*" # timedatectl list-timezones | egrep -o "Europe/L.*" # timedatectl list-timezones | egrep -o "America/N.*"
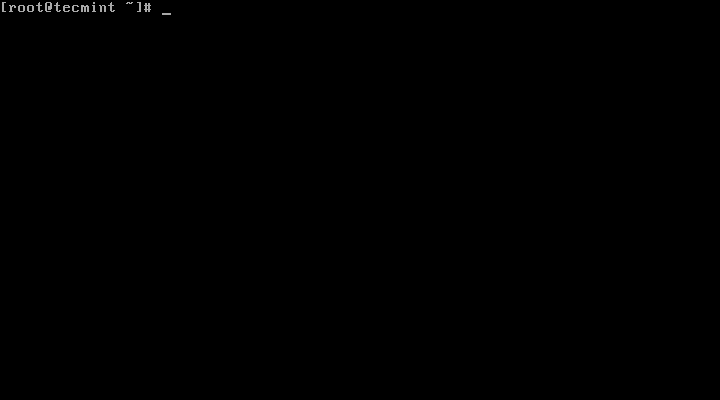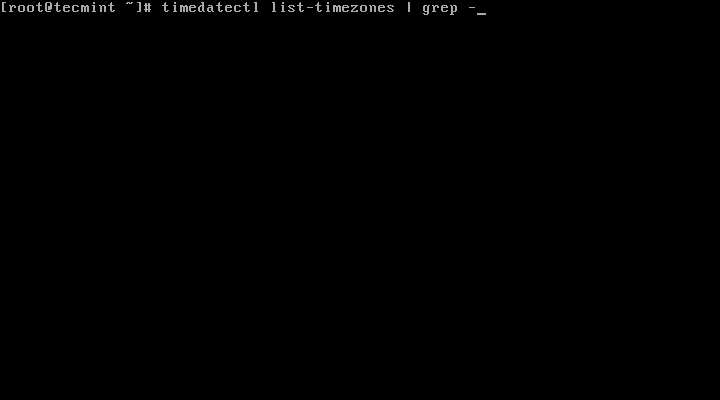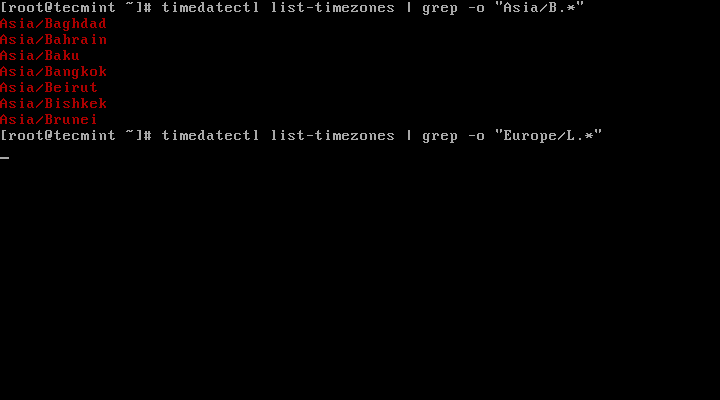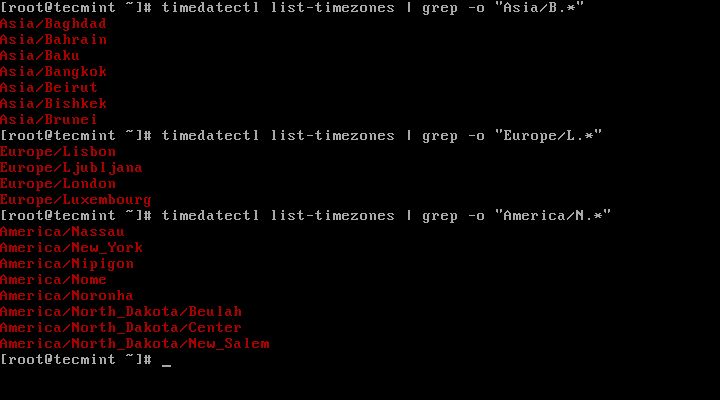
5. To set your local timezone in Linux, we will use the set-timezone switch as shown below.
# timedatectl set-timezone "Asia/Kolkata"
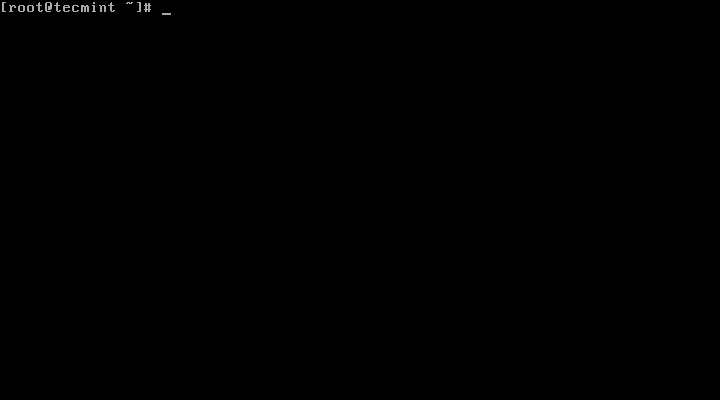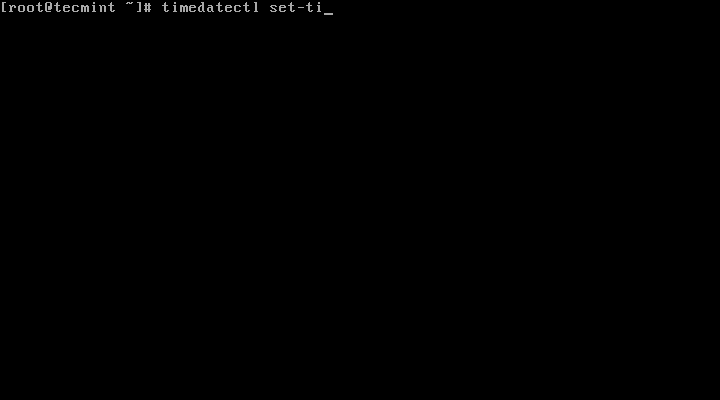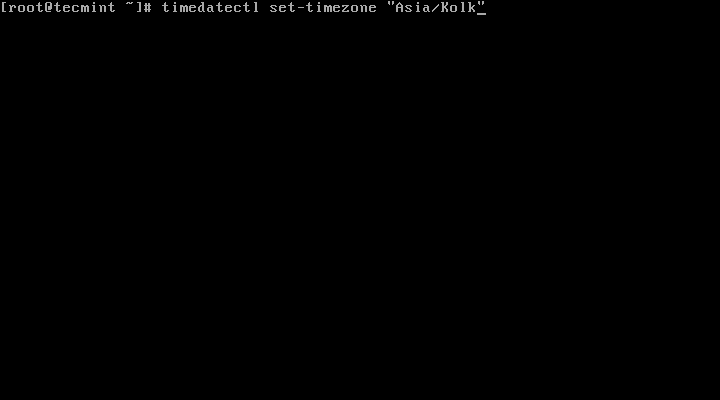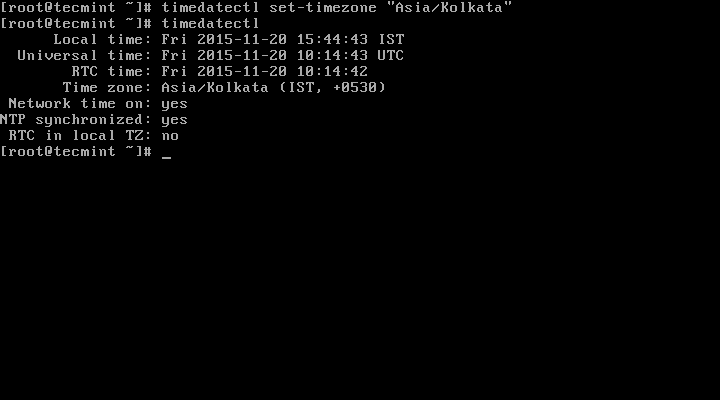
It is always recommended to use and set the coordinated universal time, UTC.
# timedatectl set-timezone UTC
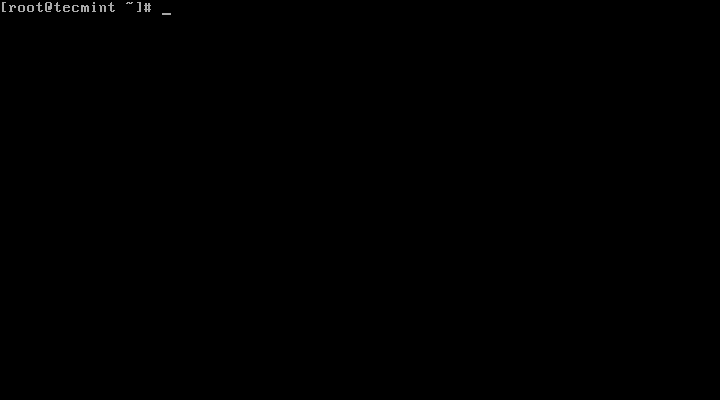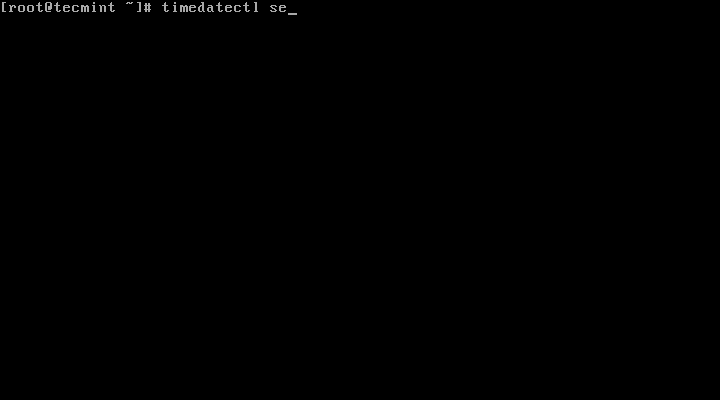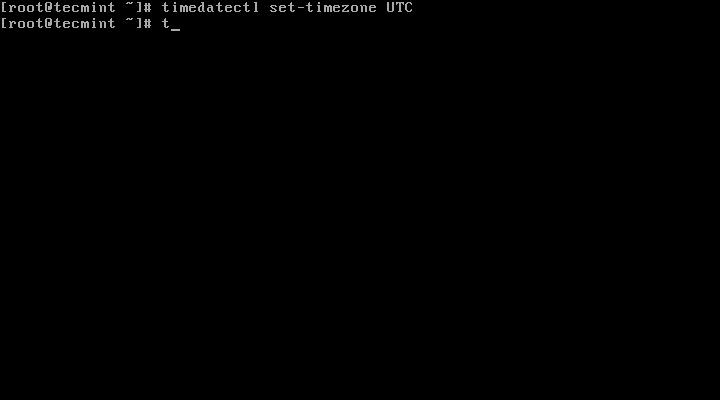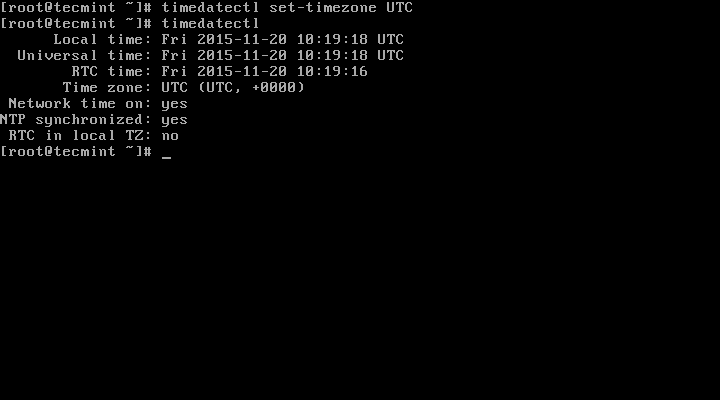
You need to type the correct name timezone otherwise you may get errors when changing the timezone, in the following example, the timezone “Asia/Kolkata” is not correct therefore causing the error.
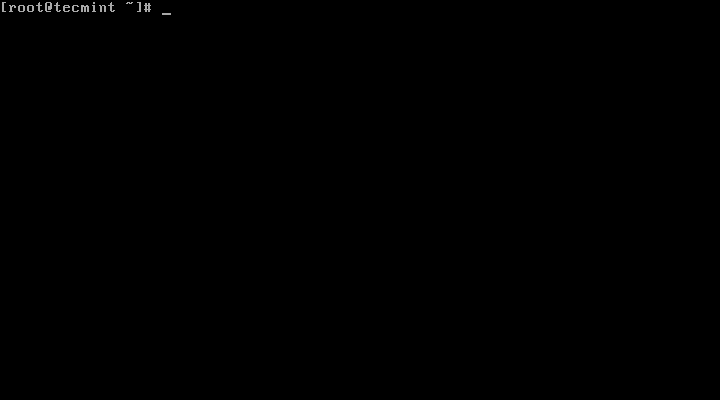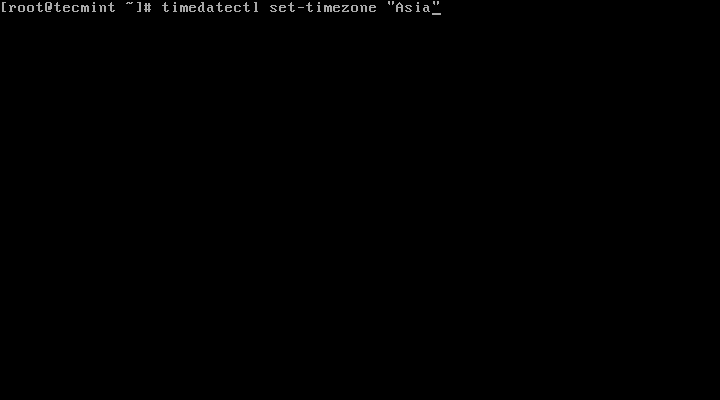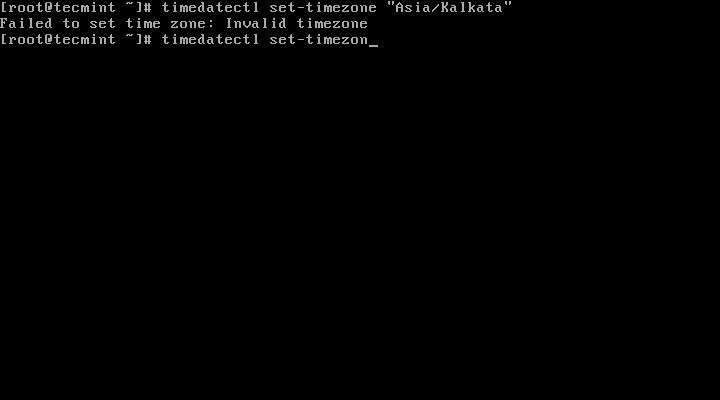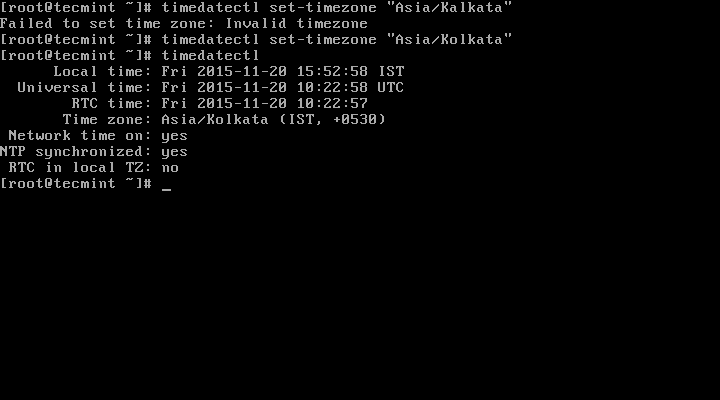
How to Set Time and Date in Linux
6. You can set the date and time on your system, using the timedatectl command as follows:
Set Time in Linux
To set time only, we can use a set-time switch along with the format of time in HH:MM:SS (Hour, Minute, and Seconds).
# timedatectl set-time 15:58:30
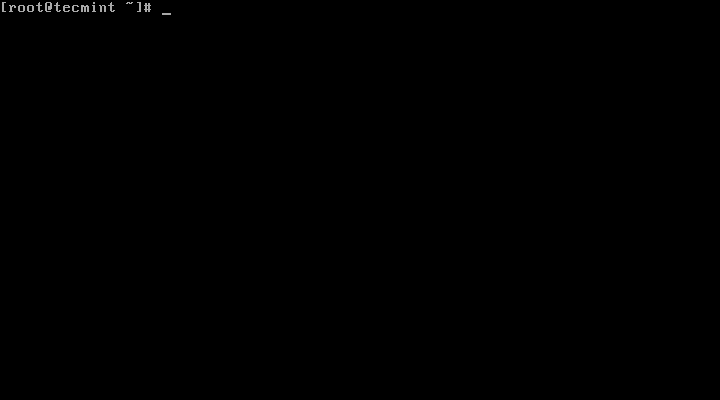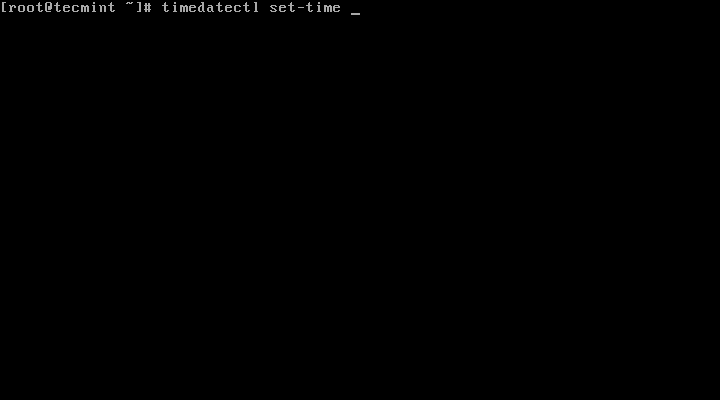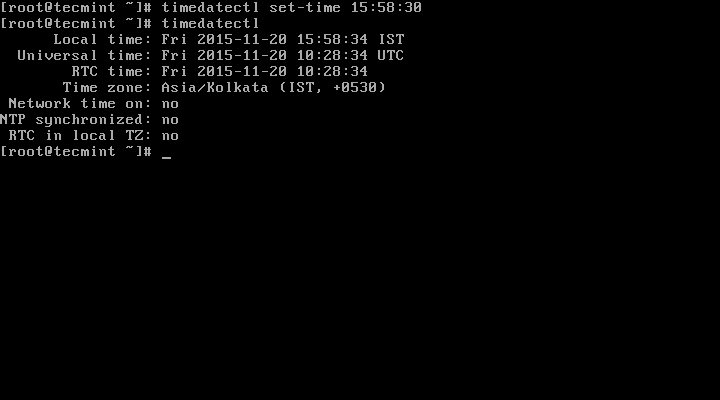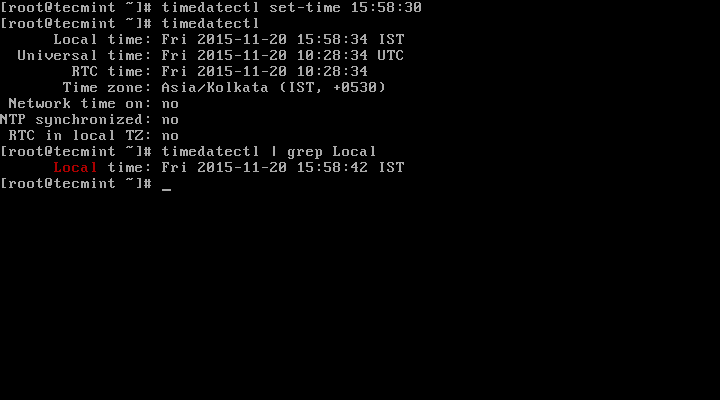
You may get the below error when setting the date as shown above:
Failed to set time: NTP unit is active
7. The error says that the NTP service is active. You need to disable it using the below command.
# systemctl disable --now chronyd
Set Date and Time in Linux
8. To set date and time, we can use a set-time switch along with the format of date in YY:MM:DD (Year, Month, Day) and time in HH:MM:SS (Hour, Minute, and Seconds).
# timedatectl set-time '2015-11-20 16:14:50'
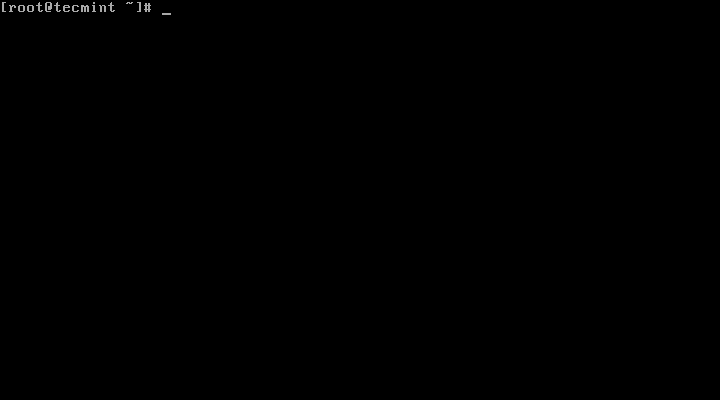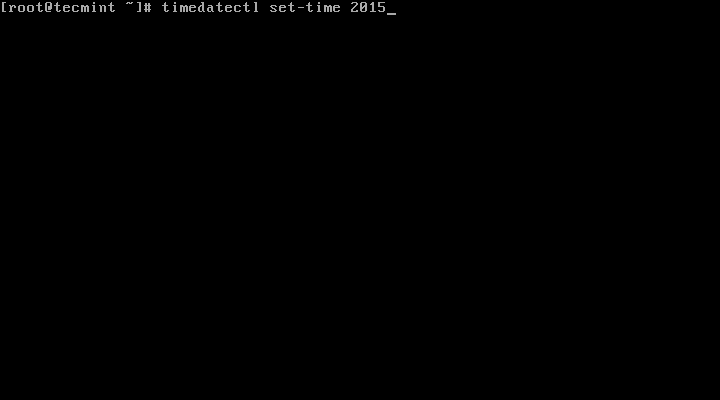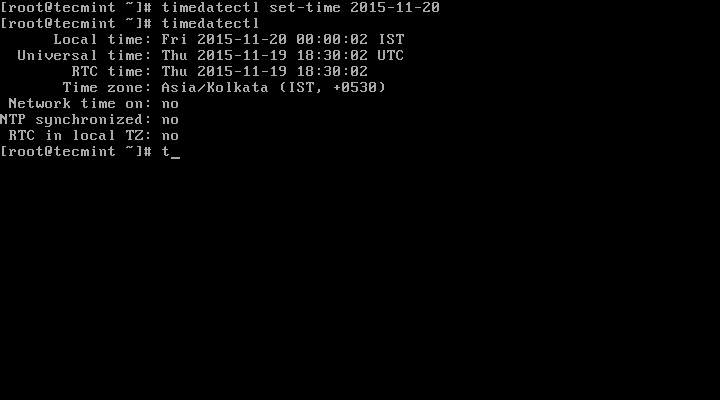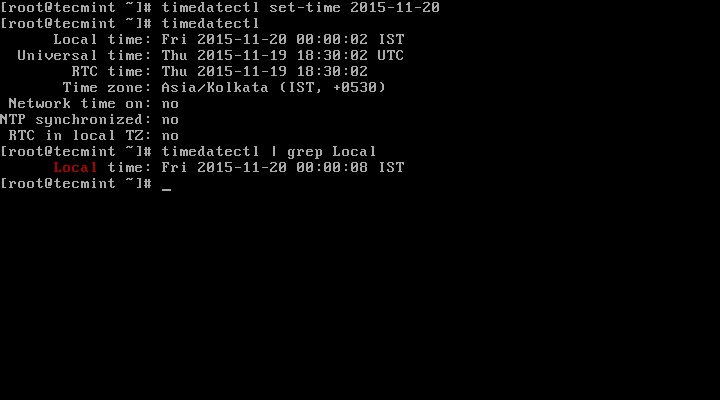
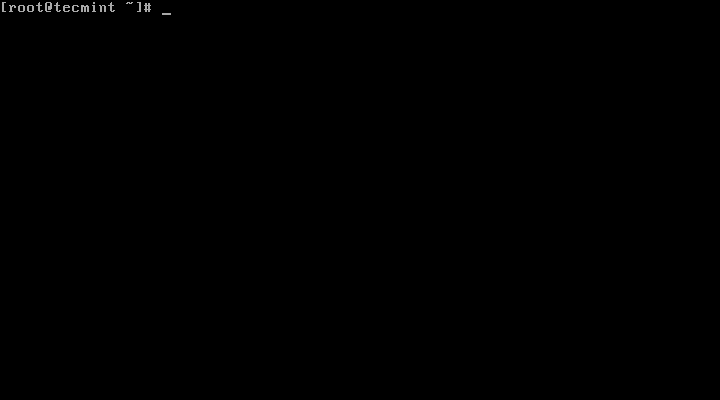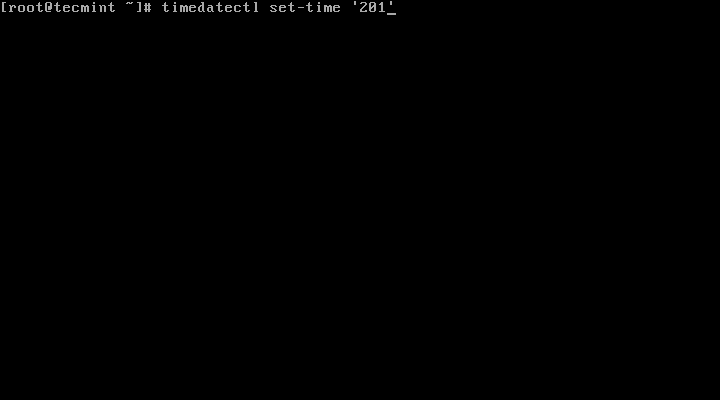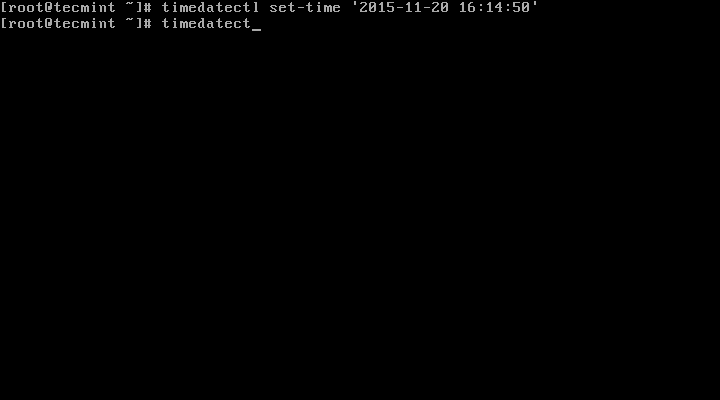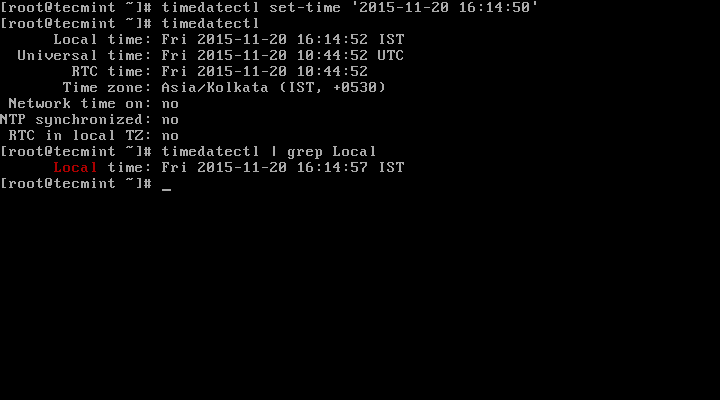
How to Find and Set Hardware Clock in Linux
9. To set your hardware clock to coordinated universal time, UTC, use the set-local-rtc boolean-value option as follows:
First Find out if your hardware clock is set to the local timezone:
# timedatectl | grep local
Set your hardware clock to the local timezone:
# timedatectl set-local-rtc 1
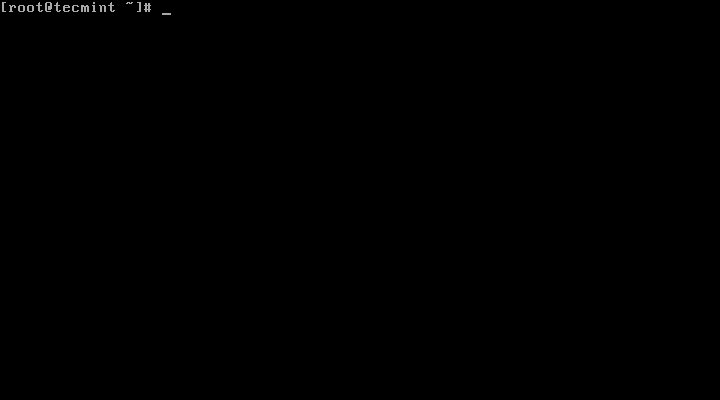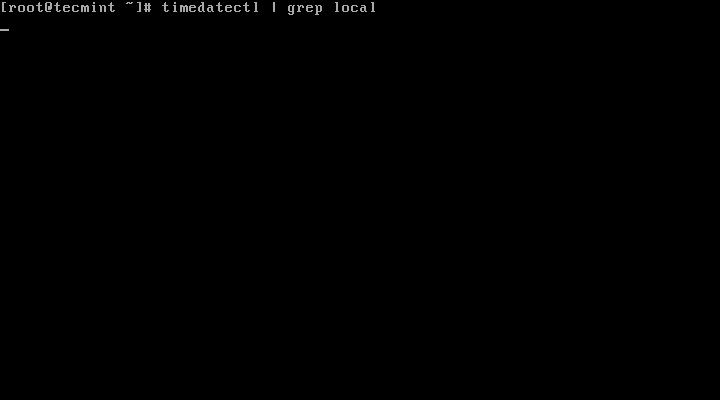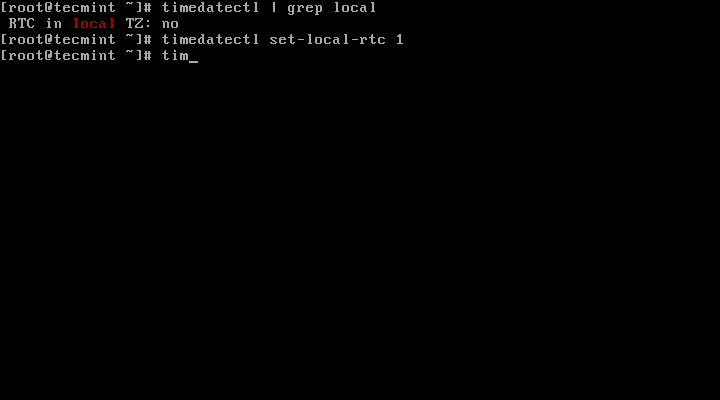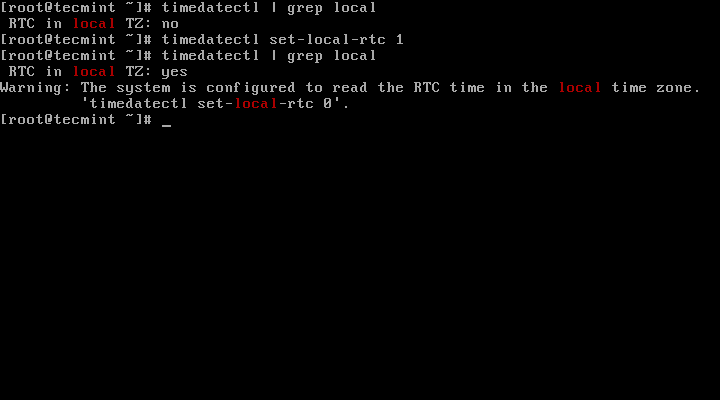
Set your hardware clock to coordinated universal time (UTC):
# timedatectl set-local-rtc 0
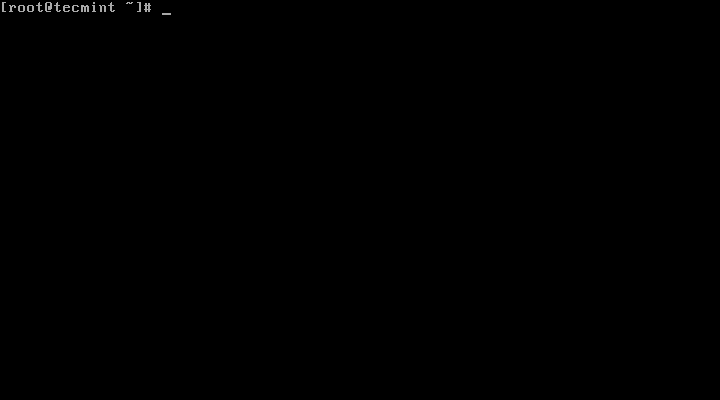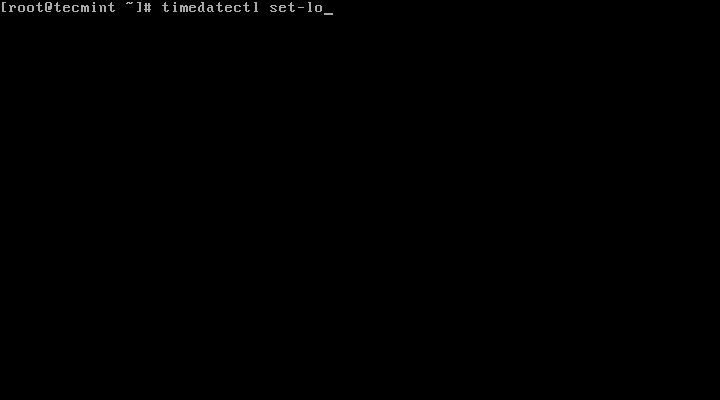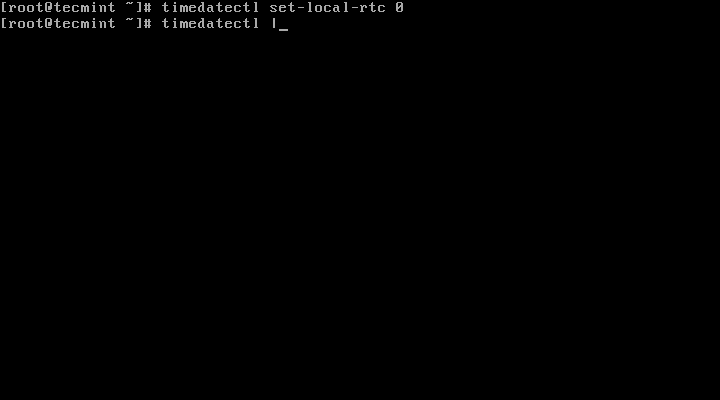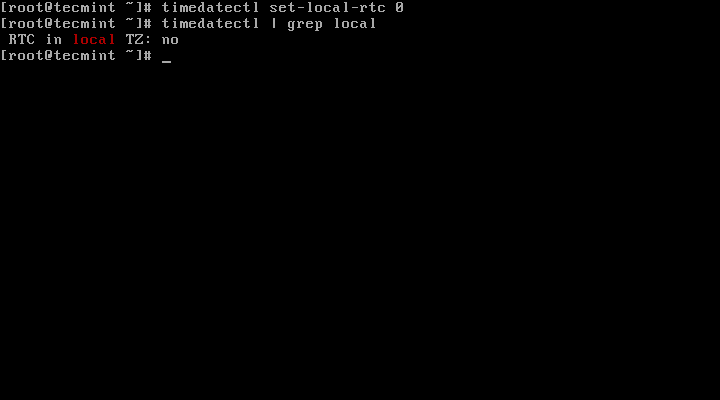
Synchronizing Linux System Clock with a Remote NTP Server
NTP stands for Network Time Protocol is an internet protocol, which is used to synchronize the system clock between computers. The timedatectl utility enables you to automatically sync your Linux system clock with a remote group of servers using NTP.
Please note that you must have NTP installed on the system to enable automatic time synchronization with NTP servers.
To start automatic time synchronization with a remote NTP server, type the following command at the terminal.
# timedatectl set-ntp true
To disable NTP time synchronization, type the following command at the terminal.
# timedatectl set-ntp false
Summary
These are very easy examples described in this tutorial and I hope you will find them helpful for setting various Linux system clocks and timezones. To learn more about this tool, head over to the timedatectl man page.
If you have anything to say about this article, feel free to leave a comment for any more information to add. Stay connected to Tecmint.




If I want to set time on different Linux machines in one go or use single command so that all of them stay in sync, is this possible?
if yes, how we can achieve this?
Good Explanation with a step-by-step process.
Impressive step-by-step instructions. The animated samples made it easy to understand.
Hi
I am facing a new issue with my server time every day it exceeds 2 seconds. Can you please suggest the server time synchronization.
root@bigdata:~# date Mon Apr 6 18:17:38 CEST 2020 root@bigdata:~# timedatectl Local time: Mon 2020-04-06 18:19:48 CEST Universal time: Mon 2020-04-06 16:19:48 UTC RTC time: Mon 2020-04-06 16:19:47 Time zone: Europe/Madrid (CEST, +0200) System clock synchronized: no systemd-timesyncd.service active: no RTC in local TZ: noI have one doubt.
Lets say if i have 2 system and both are in same time zone have “System clock synchronized: yes” or “NTP synchronized: yes” . so does it mean both systems the have exact times.
@Harshal Wagh
Yes, they should have the same time if they both have NTP client service running and synced with an NTP server.
Thanks for the examples this helped me to quickly set up ntp synchronization.
One issue found on a minimal Centos7 server install was:
The solution was to install chrony. After that the set-ntp true command worked.
@Roger
Many thanks for the useful addition.
Tip:
I had problems setting my timezone, e.g.
resulted in
though this is listed by timedatectl list-timezones.
Solution:
The actual files to which the program timedatectl puts a symlink are very few. E.g.
only lists 3 cities, one for each available timezone in Europe. So find your timezone city (e.g. Paris for Berlin, Copenhagen etc.) and set this if you encounter the same issue.
And ofcourse we set “timedatectl set-ntp true” and it magically works, but who sets the desired server, where, how. This is a big mess. Having the systemd and having to manually add the servers to the “/etc/systemd/timesyncd.conf” just looks wrong.
Also the timestamp of “/etc/systemd/timesyncd.conf” is used for the internal workings of the timedatectl and guess what, if you manually modify this file you will actually change its timestamp. Really, this is a big huge mess.
Hello,
I did the following,
But afterwards, the file /etc/systemd/timesyncd.conf, still had the Time servers commented out,
[Time]
#Servers=0.debian.pool.ntp.org 1.debian.pool.ntp.org 2.debian.pool.ntp.org 3.debian.pool.ntp.org
My question is, does the timesyncd.conf file have to be edited after running, timedatectl set-ntp true ?
Thank you.
@Brett
The default the internet cluster of ntp servers will be used. Unless you want to use the specified servers in /etc/systemd/timesyncd.conf, you can leave the time servers commented out.
Has the software been tested for edge cases, eg UTC+13?
@dn
Not to my knowledege but instead of using UTC+13, you can simply set the local timezone at UTC+13 timezone.
These animated printouts are not an improvement – it looks cute, but the user has to wait to read what interests, and goes elsewhere.
I had the very same thought about the animated examples since I came here just for a quick glance at timedatectl syntax and was turned off by visual bloat. Ironically, there’s a typo in item #8 — and the correct syntax can be seen in the GIF.